Diese Seite wird nicht mehr aktualisiert. Bitte besuchen Sie unsere neue Webpräsenz.
This page is not updated any longer. Please visit our new website.
For the majority of engineering applications, resonance and sustained oscillations can cause structural damage. The way to reduce dangerous vibrations is through damping.
Damping can also produce undesirable effects such as energy waste or heat production. On the other hand, damping is also responsible for many important system properties such as stability and dissipativity. Our investigation is devoted to optimization of damping of vibrating systems which is a very demanding problem.
Thus, our goal is to develop efficient approaches for solving problems which appear in damping optimization but also in closely connected issues such as optimality of the solution of the linear systems, stability via Lyapunov and optimal control. Another problem is the analysis of the system structure induced by the dissipativity of the system. Solving such problems is both a highly relevant and difficult task. We also investigate algorithms which can accelerate the optimization process while still ensuring accuracy.
This project will deal with optimizing certain robustness measures in order to make the controlled system robust
with respect to perturbations. Therefore, we consider
norm optimization as well as feedback stabilization
and eigenvalue assignment problems for large-scale and medium-sized dynamical systems. We will investigate the
possibility of applying a new approach for robust control of such systems based on pseudospectra.
Within the
norm optimization of large-scale dynamical systems, we will also consider optimization of the
trace of the solution of the corresponding parameter dependent Lyapunov equation. We will use a new linearized
model without a simultaneous diagonalization of the component matrices. For this problem a better understanding
of the properties of large-scale dynamical systems is required. The usage of model order reduction approaches is
investigated for this task, such that important system characteristics can be drawn at a highly reduced numerical
effort from a reduced order model. Additionally, we will derive a theory which will describe the geometry of the
corresponding eigenspaces as well as the relative perturbation bounds for corresponding eigenvalues.
For the numerical solution of the occurring matrix equation within this optimization process, we use methods
developed at the MPI Magdeburg, e.g., low-rank ADI type methods.
Regarding the feedback stabilization we will also consider the case of active damping with direct velocity
feedback, since one can obtain almost the same second order system as with passive damping. In particular, the
system:
with output 
and an active control 
leads to
. Since the system is almost the same as in the investigation of
passive damping, we investigate if some of our existing results can also be applied in active damping.
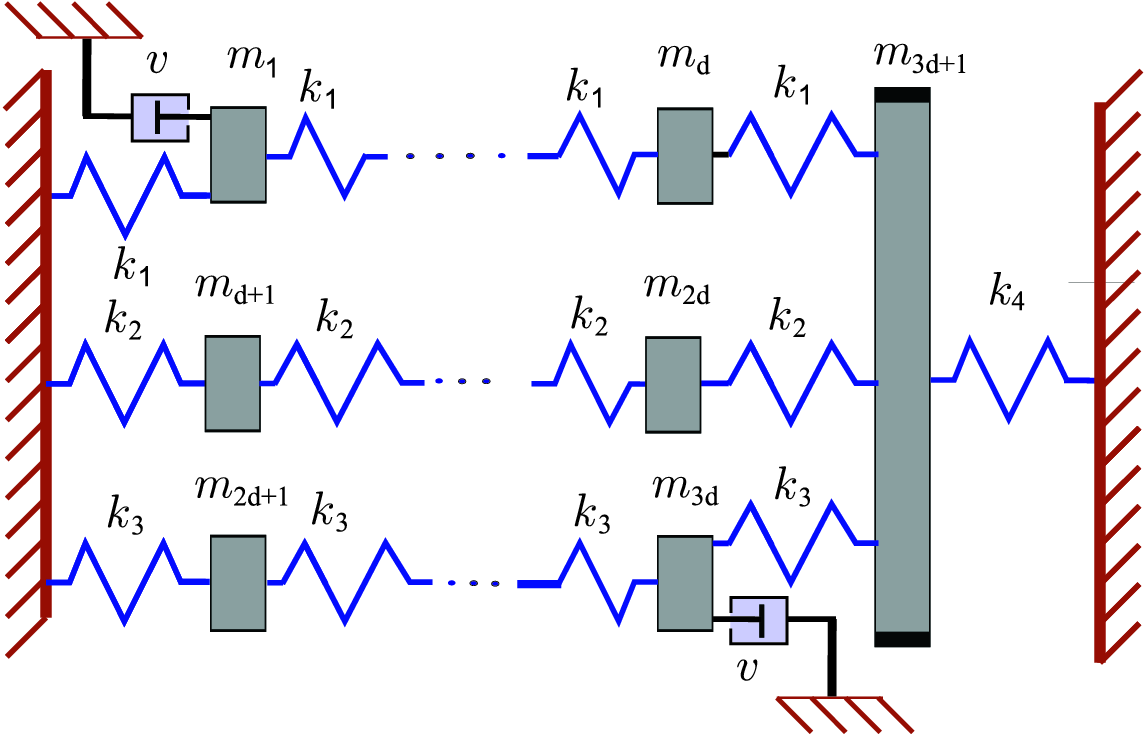 Second order mechanical system |
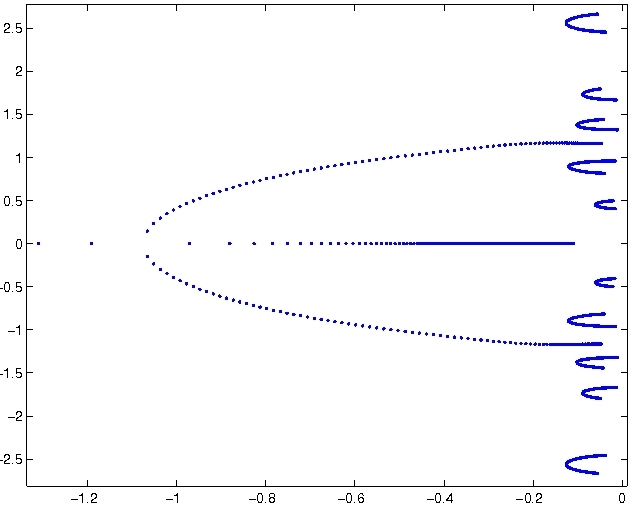 Eigenvalue behavior for fixed damper position with varying viscosity |
@arcticle{BenKTT14, author = {Peter Benner and Patrick K{\"u}rschner and Zoran Tomljanovi\'{c} and Ninoslav Truhar}, title = {Semi-active damping optimization of vibrational systems using the parametric dominant pole algorithm}, month = {July} year = 2016, journal={ZAMM}, volume=96, number=5, pages={604--619} } | Semi-active damping optimization of vibrational systems using the parametric dominant pole algorithm; Benner, Peter; Kürschner, Patrick; Tomljanović, Zoran; Ninoslav, Truhar;; ZAMM : 96(5), pp. 604-619; WILEY-VCH; 2016. |
J. Denißen
Trigonometric spline approximation bounds on the solution of linear time-periodic systems,
Seminar on Optimization and Applications at Josip Juraj Strossmayer University Osijek, Osijek, Croatia, March 13, 2013