Diese Seite wird nicht mehr aktualisiert. Bitte besuchen Sie unsere neue Webpräsenz.
This page is not updated any longer. Please visit our new website.
Model Order Reduction for Chromatographic Processes
Project Coordinator:
- Prof. Dr. Peter Benner
Max Planck Institute for Dynamics of Complex Technical Systems,
Computational Methods in Systems and Control Theory,
Tel: +49 (0)391-6110-451
E-mail: benner@mpi-magdeburg.mpg.de
Researcher:
- Dr. Lihong Feng
Max Planck Institute for Dynamics of Complex Technical Systems Magdeburg,
Computational Methods in Systems and Control Theory,
Tel: +49 (0)391-6110-379
E-mail: feng@mpi-magdeburg.mpg.de
- Dr. Suzhou Li
Max Planck Institute for Dynamics of Complex Technical Systems Magdeburg,
Computational Methods in Systems and Control Theory,
Tel: +49 (0)391-6110-367
E-mail: suzhou@mpi-magdeburg.mpg.de
- Dr. Yao Yue
Max Planck Institute for Dynamics of Complex Technical Systems Magdeburg,
Computational Methods in Systems and Control Theory,
Tel: +49 (0)391-6110-433
E-mail: yue@mpi-magdeburg.mpg.de
- M.Sc. Yongjin Zhang
Max Planck Institute for Dynamics of Complex Technical Systems Magdeburg,
Computational Methods in Systems and Control Theory,
Tel: +49 (0)391-6110-807
E-mail: zhangy@mpi-magdeburg.mpg.de
Duration and Funding:
- since 04/2011, MPI Magdeburg
Project Description:
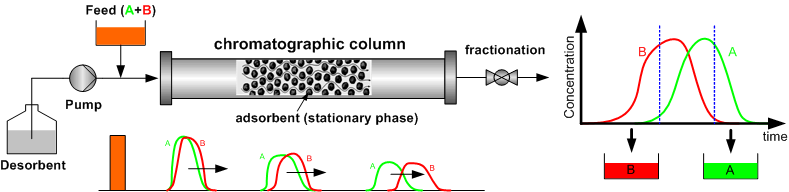
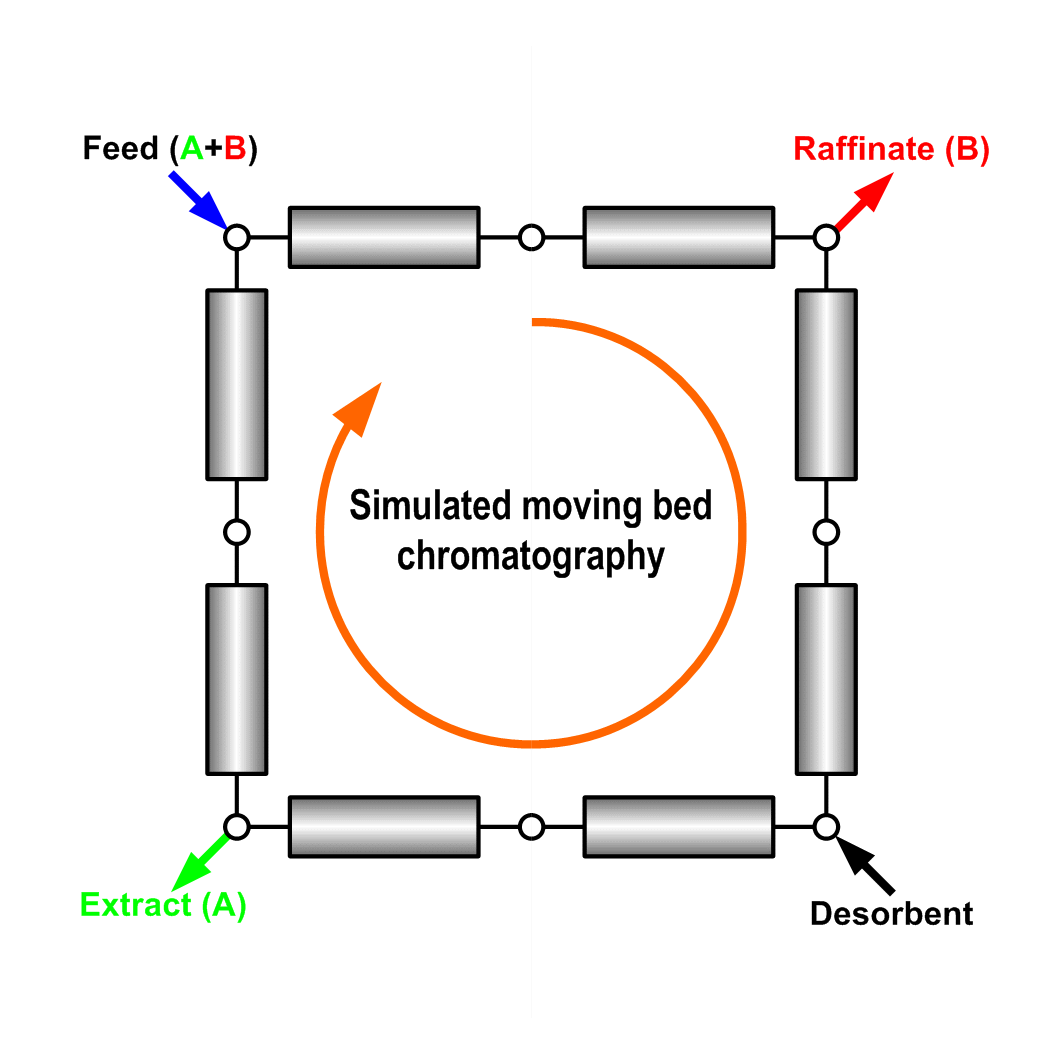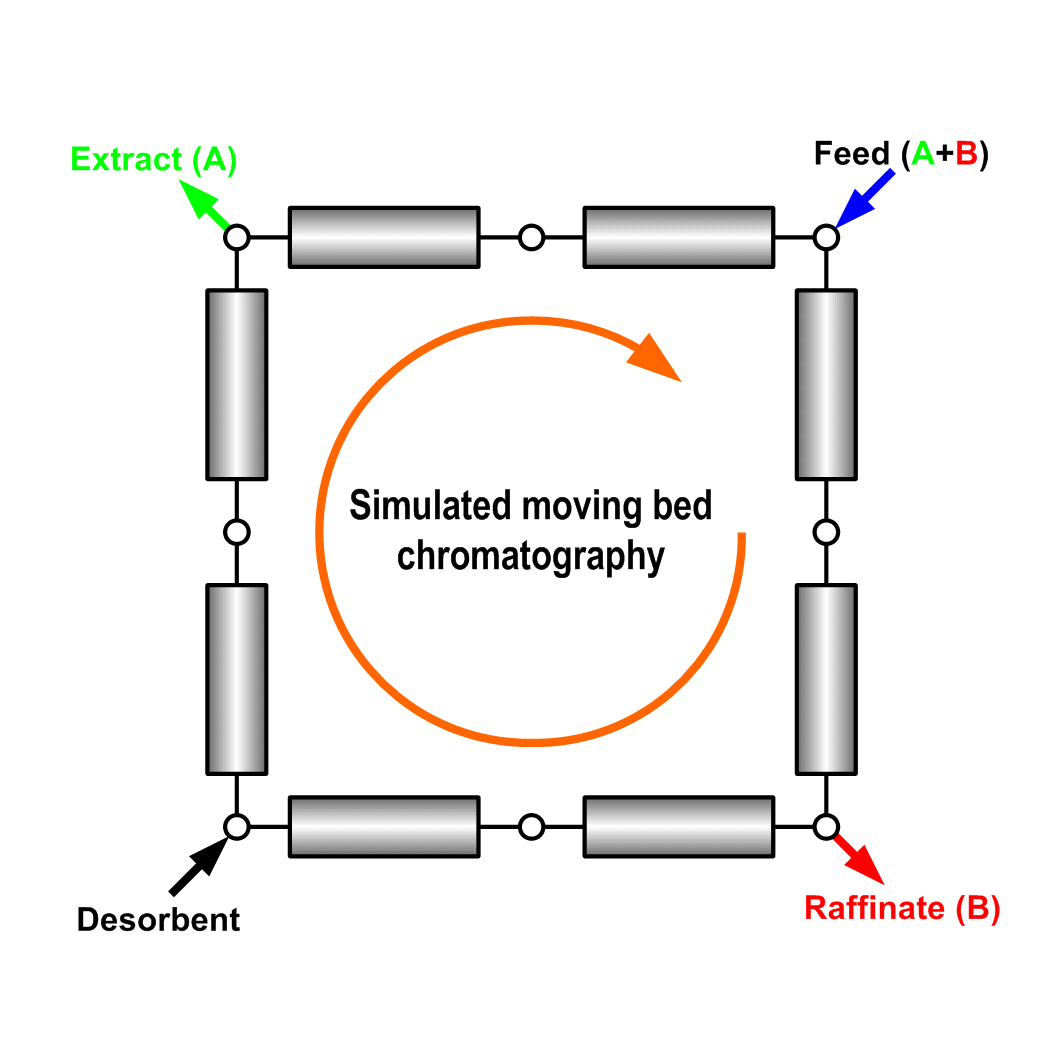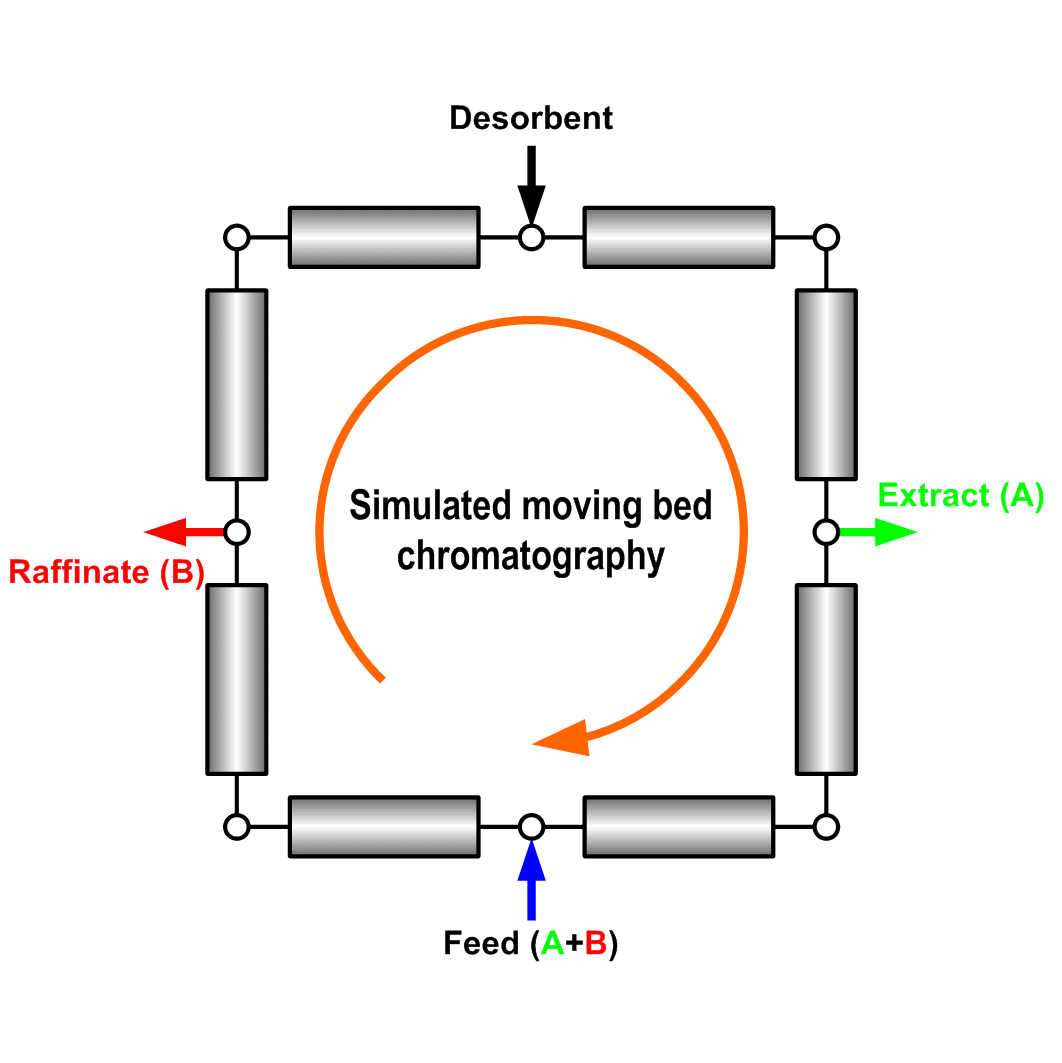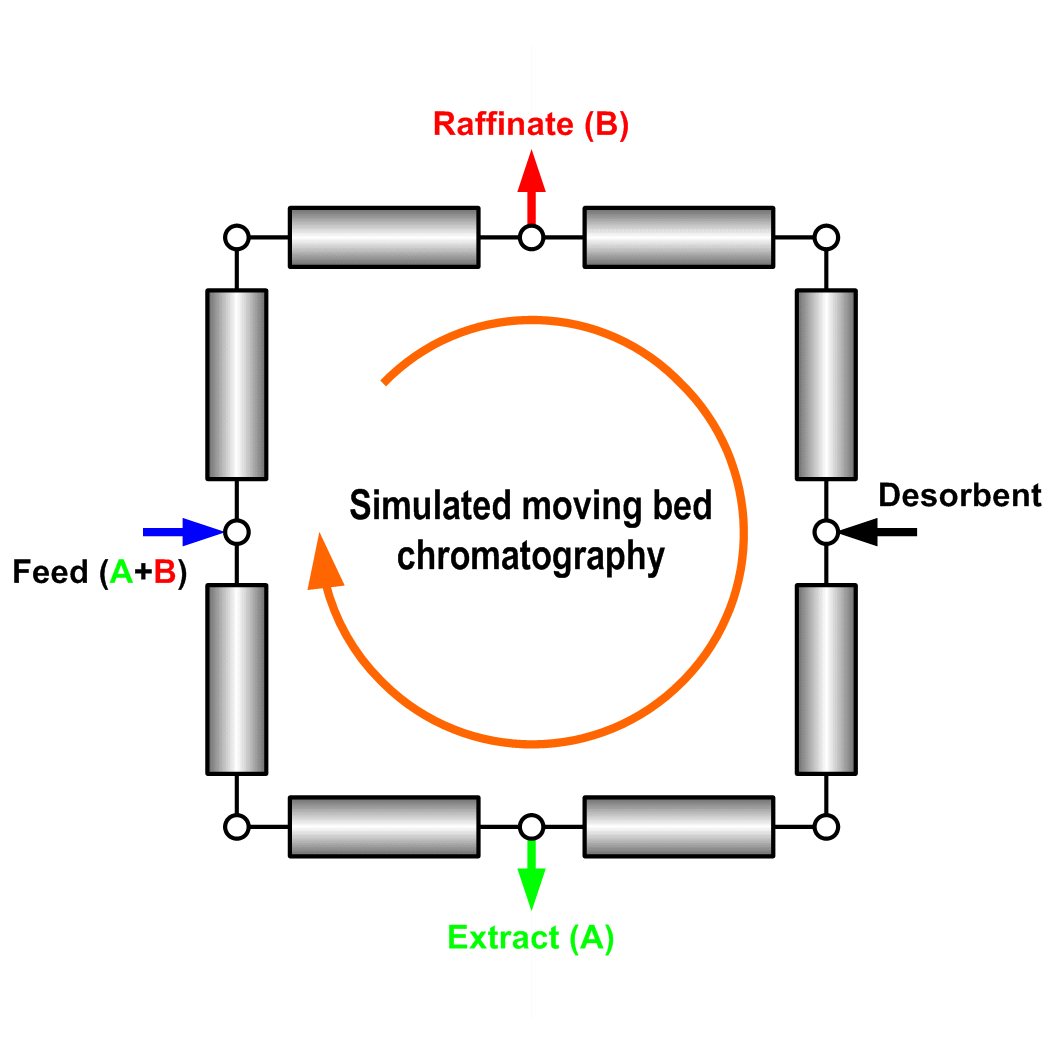
Preparative liquid chromatography as an efficient separation technique nowadays has gained great popularity in petrochemical, fine chemical and pharmaceutical industries. The separation can often be operated in either batch elution (Fig. 1) or continuous manner, such as simulated moving bed (SMB) chromatography (Fig. 2).
 |
 |
| Fig. 1: Schematic diagram of a batch chromatographic process for a binary
separation of A and B. |
Fig. 2: Schematic illustration of a simulated moving bed (SMB)
chromatographic process with 4 zones and 8 columns. |
For each case the process is generally governed by highly coupled and nonlinear partial differential equations (PDEs), which poses a significant challenge to model-based research activities, such as simulation, parameter estimation, optimization as well as control problems. In cooperation with the group of
Prof. Seidel-Morgenstern, this project focuses on systematic studies of model reduction schemes for both types of chromatographic processes. The primary aim is to reduce complexity from the model level and to contribute computationally cheap reduced-order models (ROMs) for this specific field of process system engineering. By combining the expertise of the two groups, we want to:
apply well-established model order reduction (MOR) approaches
develop new model reduction strategies
evaluate performance of ROMs systematically
identify applicability and effectiveness of various MOR algorithms
Recent Progress:
Model order reduction
We explore both snapshot-based model reduction strategies and those that are not based on snapshot sets.
1. POD approach
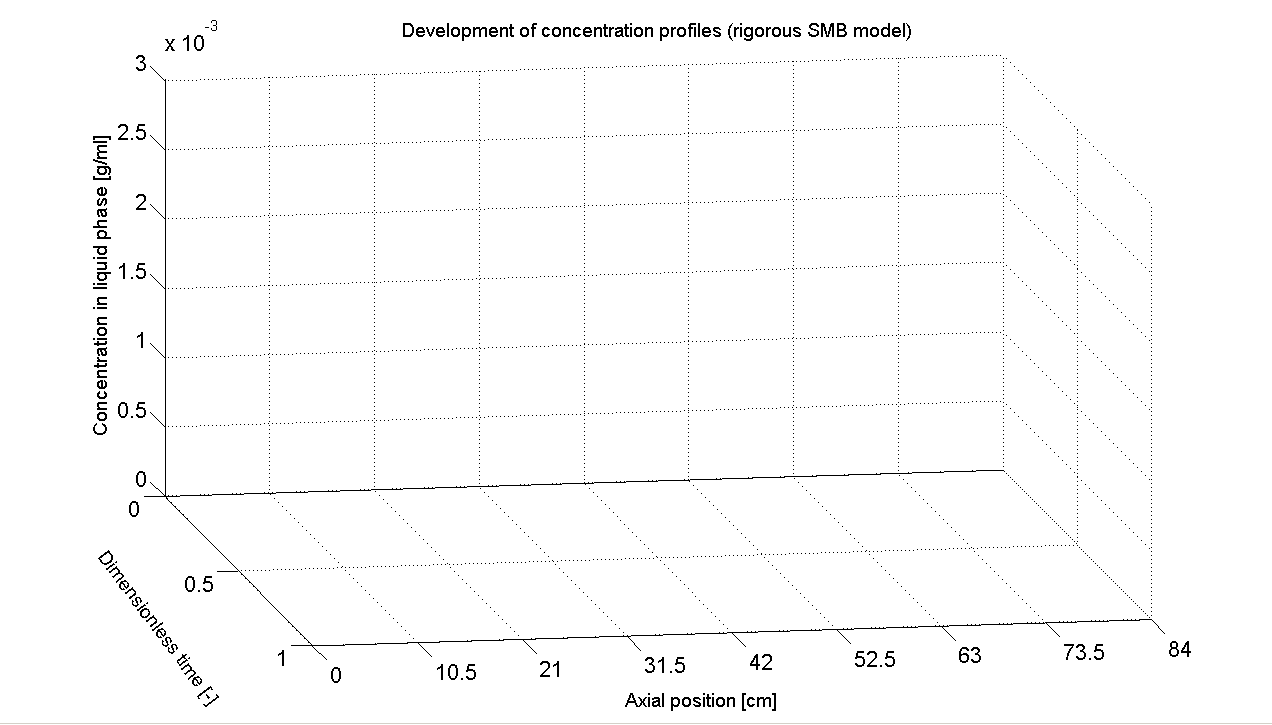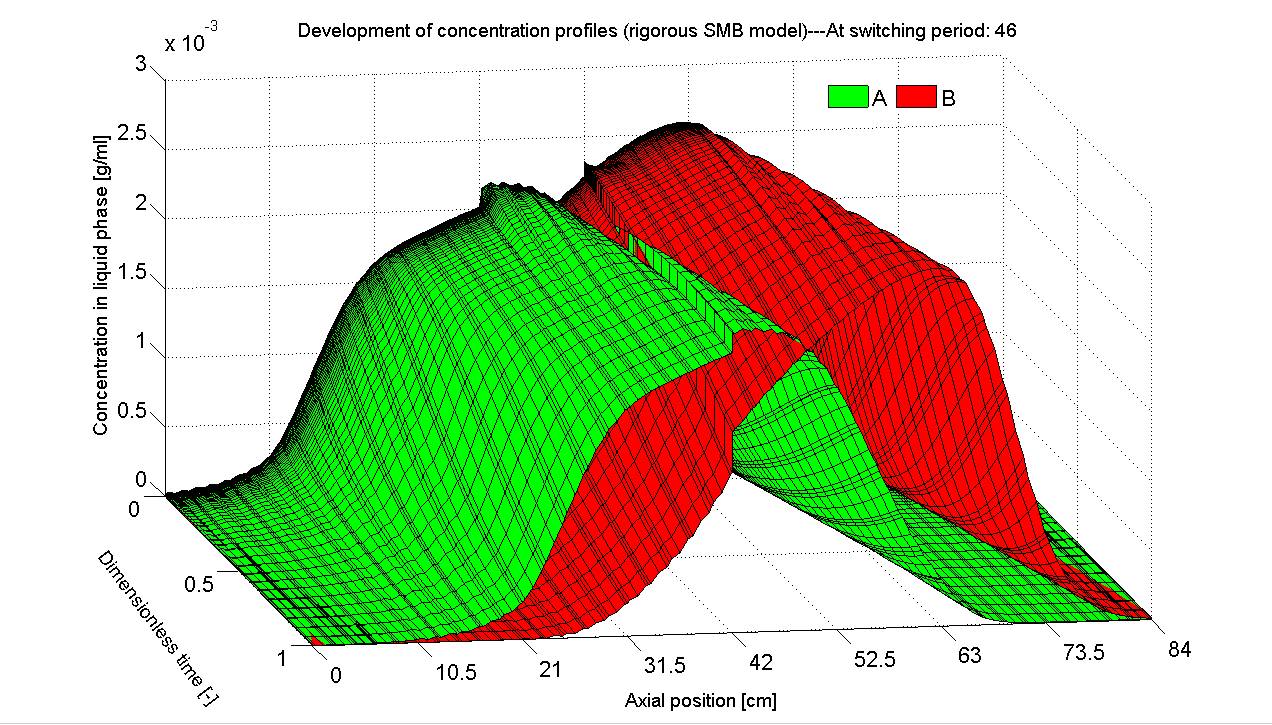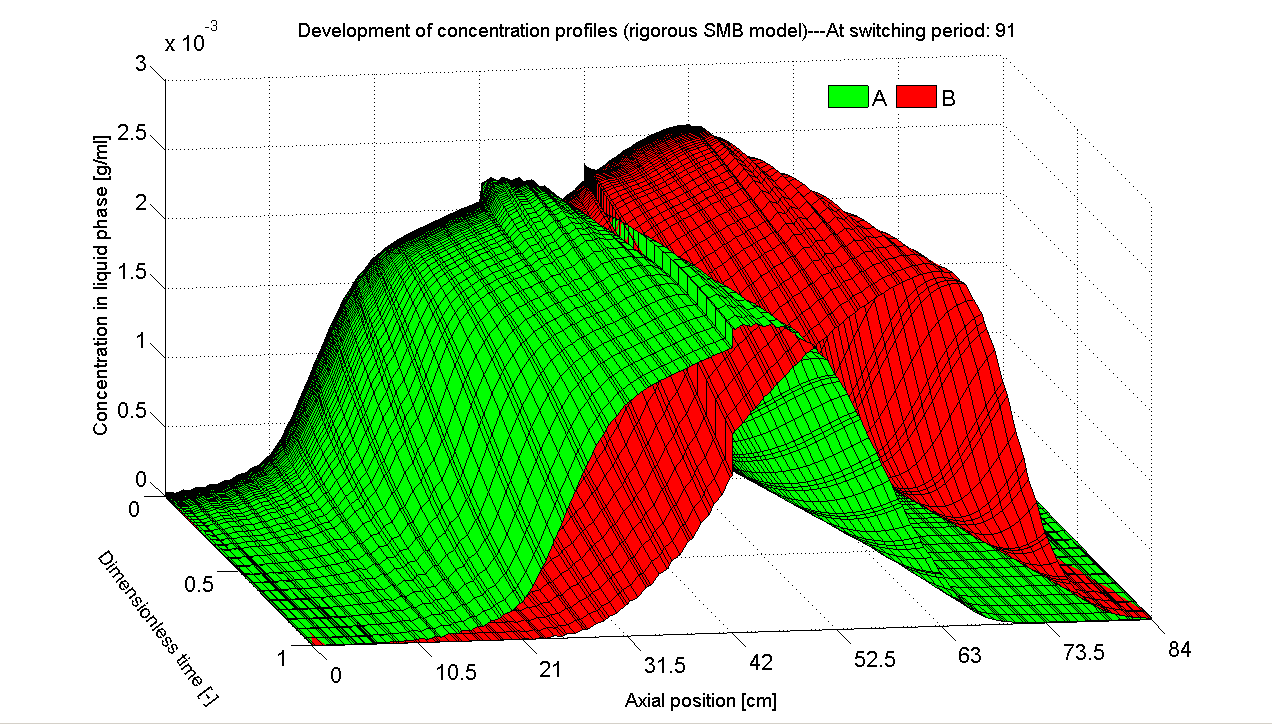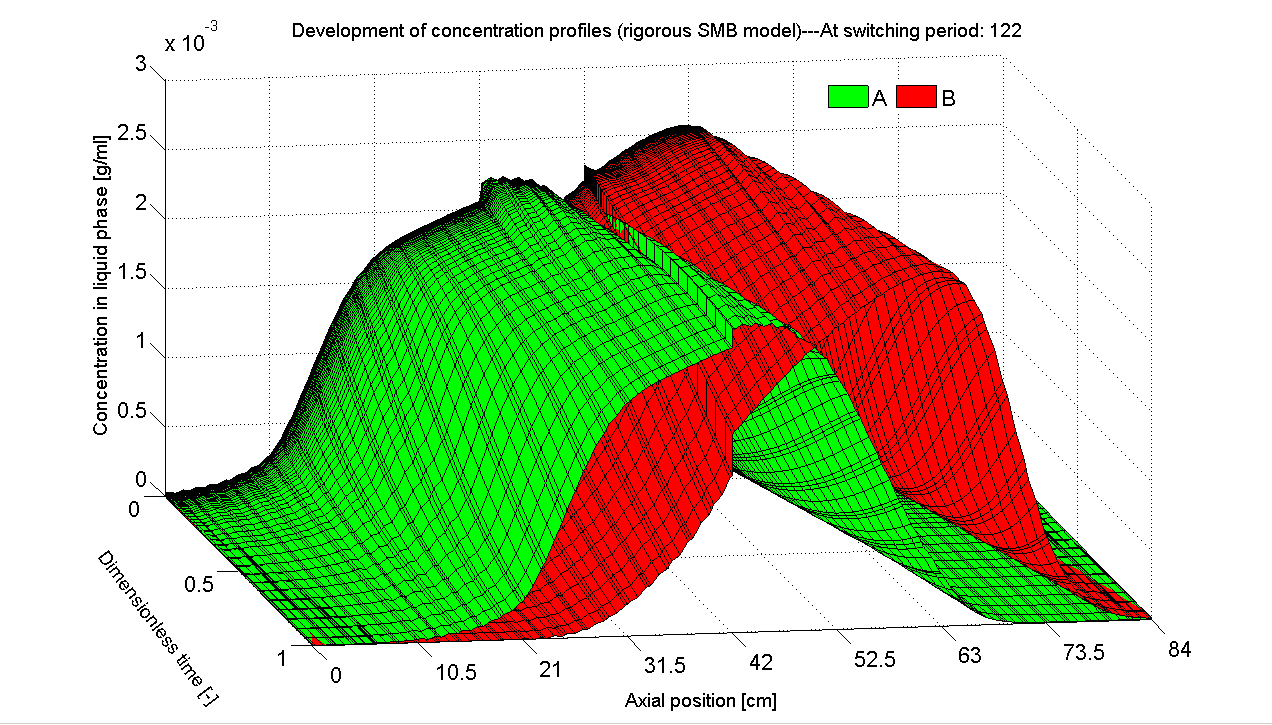
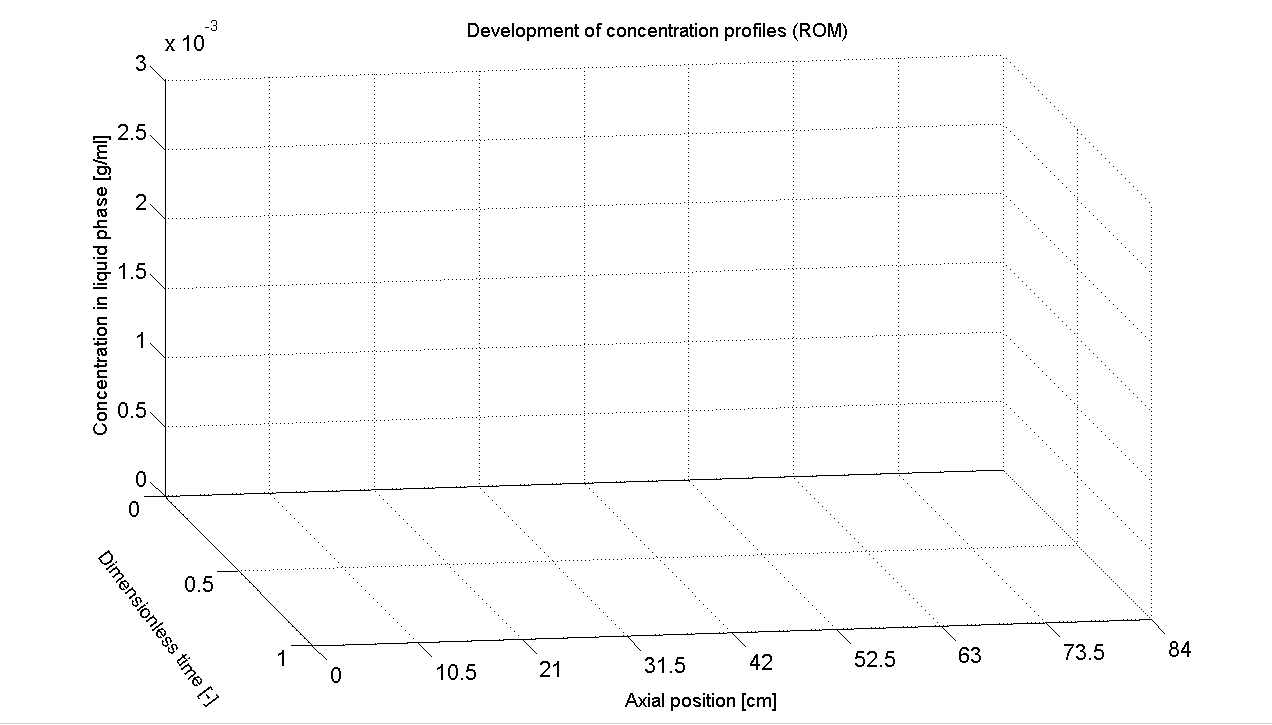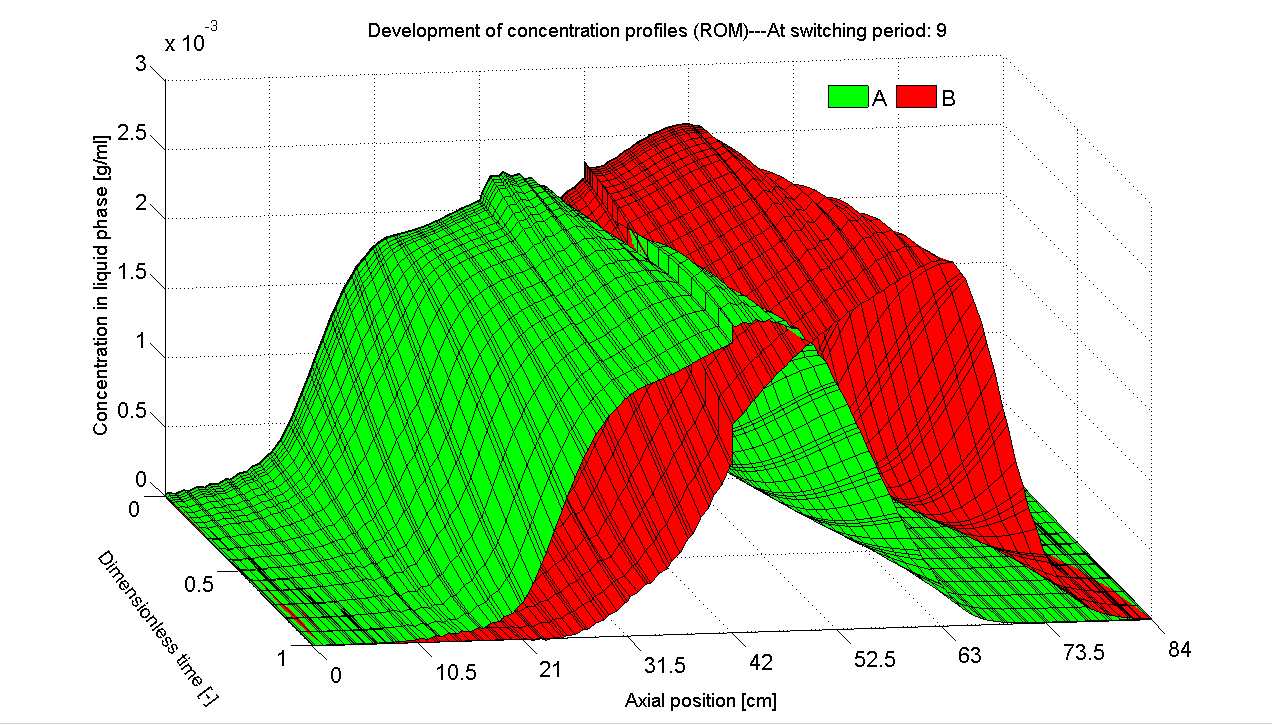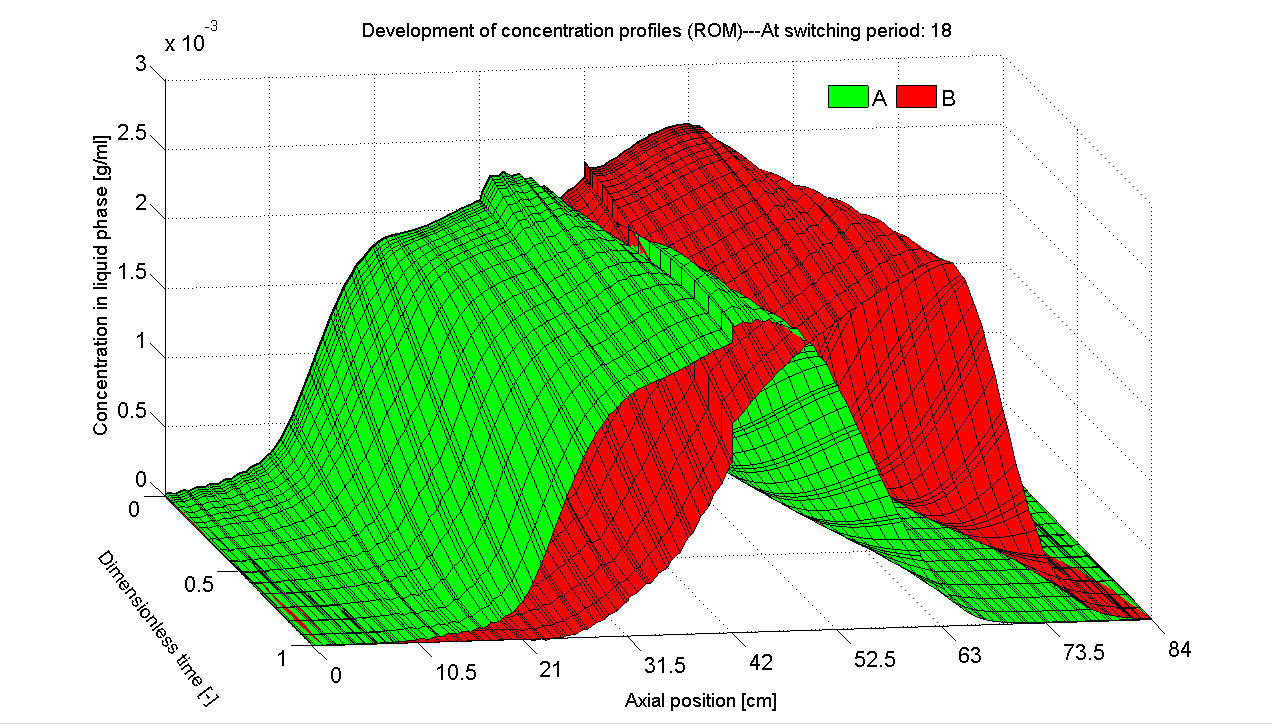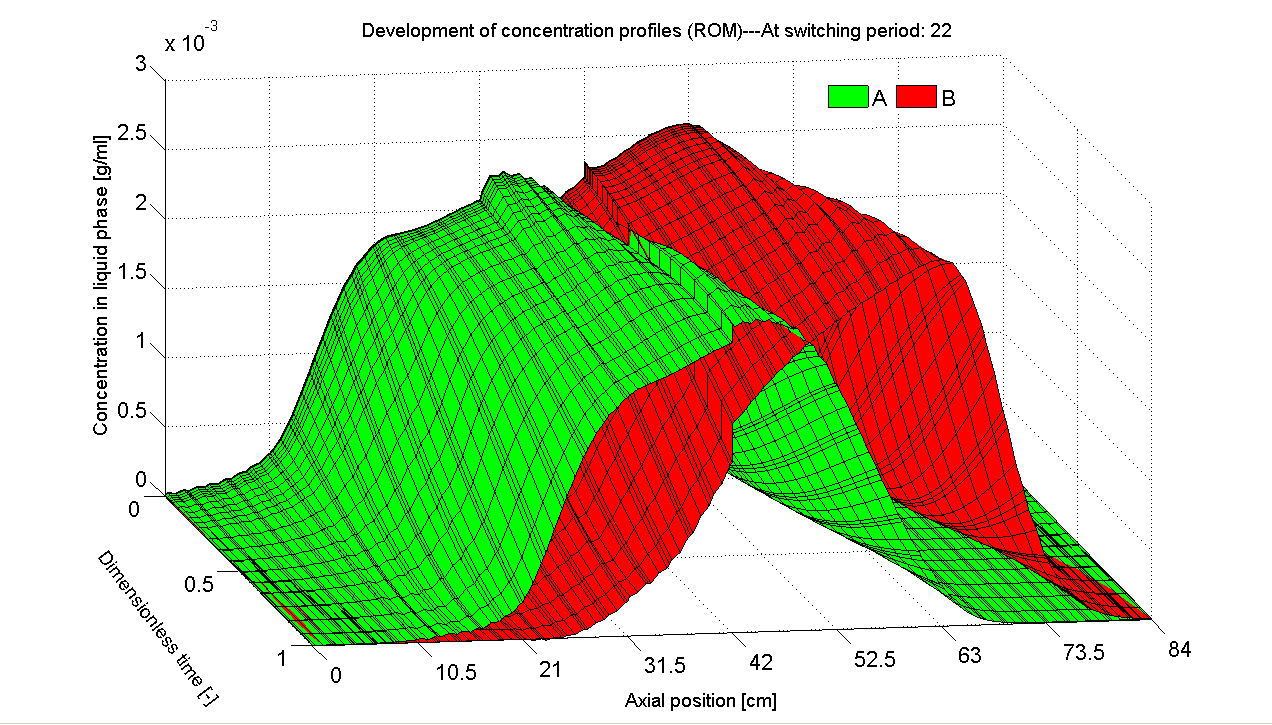
POD has been proven a powerful MOR tool for nonlinear systems and found a wide variety of applications. The great success and popularity motivates us firstly to employ it to construct ROMs. For the SMB process, we collect the cyclic steady state (CSS) solution of the original full-order model as the snapshot set. Based on this data set we derive POD-based ROMs. It is found that the ROM has a significant lower order and is able to reproduce the original CSS dynamics accurately (Figs. 3 and 4).
 |
 |
| Fig. 3: Development of axial concentration profiles of the full-order DAE
model with order of 672. |
Fig. 4: Axial concentration profiles reproduced by POD-based ROM (with
reduced order of only 2). |
Although POD has ability to deal with the nonlinearity arising from the nonlinear adsorption behavior in the processes, we also note its drawbacks, such as
solution of the original full-order system is required to generate snapshots
validity of a ROM is restricted to a neighborhood of the reference point at which the model is derived
This motivates us to explore other alternative model reduction approaches.
2. Reduced basis method
Reduced basis method (RBM) is a robust parametric MOR technique, and has been widely used for
linear or nonlinear problems in many applications. It is often endowed with an a posteriori error estimation,
which is used for the generation of the reduced basis and qualification of the resulting ROM.
The RBM is employed to generate a parametric ROM for batach chromatogrphic model,
which is reliable in the whole parameter domain and is applied to accelerate the optimization of batch
chromatography. In addition,
an adaptive technique of snapshot selection is proposed to reduce the cost of the generation of the ROM
an output-oriented error estimation is derived in the vector space for the evolution equations, and is applied
to the RBM for batch chromatography
3. Krylov subspace algorithm
Currently we restrict our efforts to the scenario where adsorption isotherms are linear. For this special class of system, we have not only investigated the standard Krylov subspace method but also developed a novel block algorithm. We have compared the performance of ROMs built based upon the two approaches for the SMB process.
| Table 1: Comparison of CSS simulation results of full-order model and ROMs
constructed by Krylov subspace approaches. |
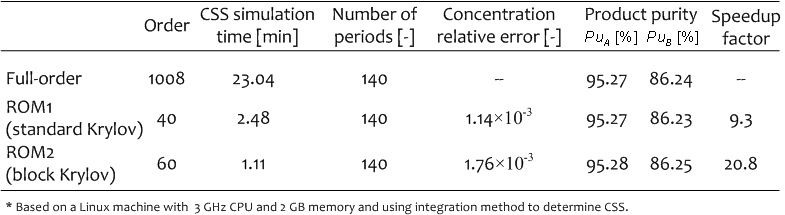 |
For a fructose-glucose separation example characterized by linear isotherm, the CSS simulation results obtained from the full-order DAE model and ROMs are summarized in Table 1. It is clearly illustrated that both algorithms yield high-quality ROMs that have the largely reduced orders while fulfilling our accuracy requirements. With the help of the ROMs, the CSS simulation can be significantly accelerated, and both product purities can also be predicted precisely.
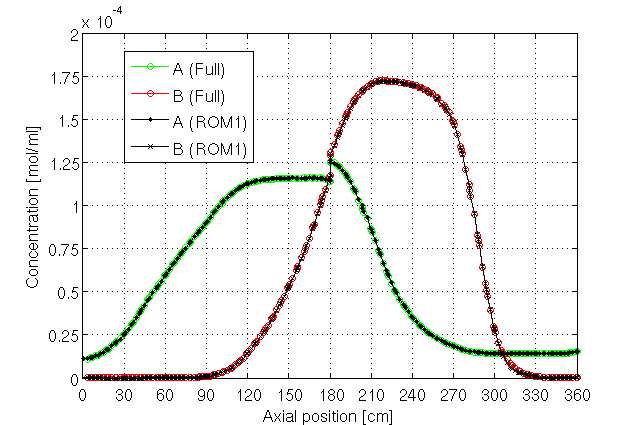 |
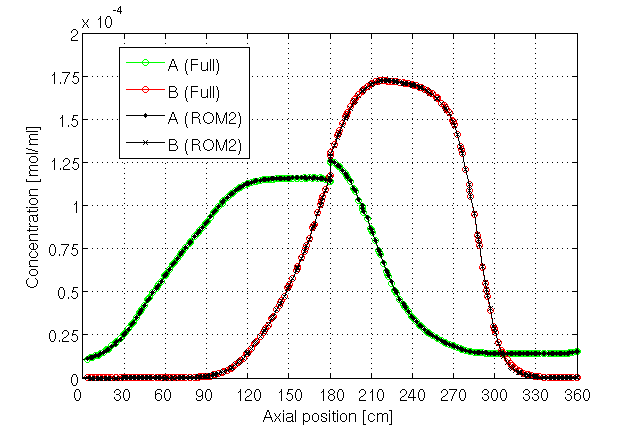 |
| Fig. 5: Comparison of CSS axial concentration profiles (full-order SMB model
v.s. ROM1). |
Fig. 6: Comparison of CSS axial concentration profiles (full-order SMB model
v.s. ROM2). |
In the future, we will extend our work to systems characterized by nonlinear isotherms. The special emphasis will be focused on how to linearize the isotherm equations.
ROM-based applications
An efficient way to evaluate the quality of a ROM is to use it for various model-based applications. We are specially interested in using our ROMs to accelerate steady state optimization of the chromatographic processes under consideration, since conventional optimization procedures based on full-order models often are expensive. For POD-based ROMs, we have used the trust-region algorithm to manage them during the course of optimization. The algorithm restricts the amount of optimization performed with one ROM, and provides an adaptive ROM update mechanism as the optimization proceeds. It is shown that the new ROM-based optimization method not only converges to the optimum obtained with the full-order model, but also leads to significant computational savings.
Related Publications:
Suzhou Li, Lihong Feng, Peter Benner and Andreas Seidel-Morgenstern, Efficient optimization of simulated moving bed processes using reduced order models, Computer Aided Chemical Engineering 30 (2012) 1232-1236.
Suzhou Li, Lihong Feng, Peter Benner and Andreas Seidel-Morgenstern, Using surrogate models for efficient optimization of simulated moving bed chromatography, to be submitted to Computers & Chemical Engineering, 2013.
Posters:
Suzhou Li, Lihong Feng, Peter Benner and Andreas Seidel-Morgenstern, Using surrogate models for efficient optimization of simulated moving bed chromatography, 14th International Symposium on Preparative and Industrial Chromatography and Allied Techniques, Brussels, Belgium, 2012.
Presentations and Talks:









