Diese Seite wird nicht mehr aktualisiert. Bitte besuchen Sie unsere neue Webpräsenz.
This page is not updated any longer. Please visit our new website.
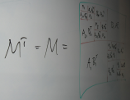
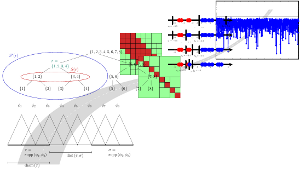Große
dicht-besetzte Matrizen sind oftmals zu groß um mit Standardalgorithmen
verarbeitet zu werden. Mit Hilfe spezieller Algorithmen, welche die Struktur der
Matrizen ausnutzen, ist dies jedoch möglich. Wir untersuchen Matrizen mit
hierarchischer Rang Struktur (siehe [1]) und mit
Tensor-Train Struktur (siehe [2]). @Article{BenM12, author = {P. Benner and T. Mach}, title = {The Preconditioned Inverse Iteration for Hierarchical Matrices}, year = 2013, journal = {Numer. Lin. Alg. Appl.}, doi = {10.1002/nla.1830}, pages = {150--166}, volume=20, number=1 } | The Preconditioned Inverse Iteration for Hierarchical Matrices; Benner, Peter; Mach, Thomas; Numer. Lin. Alg. Appl. : Vol. 20, No. 1, 150-166; 2013. DOI: 10.1002/nla.1830 also available as preprint MPIMD/11-01, 17 pages. |
@Article{BenM12b, author = {Peter Benner and Thomas Mach}, title = {Computing All or Some Eigenvalues of Symmetric $\mathcal{H}_{\ell}$-Matrices}, publisher = {SIAM}, year = {2012}, journal = {SIAM Journal on Scientific Computing}, volume = {34}, number = {1}, pages = {A485-A496}, keywords = {symmetric hierarchical matrices; eigenvalues; $\mathcal{H}_{\ell}$-matrices; slicing the spectrum}, url = {https://link.aip.org/link/?SCE/34/A485/1}, doi = {10.1137/100815323} } | Computing all or some Eigenvalues of symmetric ℋℓ-Matrices; Benner, Peter; Mach, Thomas; SIAM Journal of Scientific Computing : Vol. 34, No. 1, A485-A496; 2012. DOI: 10.1137/100815323 also available as preprint MPIMD/10-01. |
@TECHREPORT{MPIMD12-05, author = {Peter Benner and Thomas Mach}, title = {The LR Cholesky Algorithm for Symmetric Hierarchical Matrices}, number = {MPIMD/12-05}, month = {February}, year = 2012, type = {MPI Magdeburg Preprint}, note = {Available from \url{https://www.mpi-magdeburg.mpg.de/preprints/}}, } | The LR Cholesky Algorithm for Symmetric Hierarchical Matrices; Benner, Peter; Mach, Thomas ; 2012. available as preprint MPIMD/12-05, 16 pages. |
@TECHREPORT{MPIMD11-09, author = {Thomas Mach}, title = {Computing Inner Eigenvalues of Matrices in Tensor Train Matrix Format}, institution = {Max Planck Institute Magdeburg Preprints}, year = 2011, number = {MPIMD/11-09}, month = {December} } | Computing Inner Eigenvalues of Matrices in Tensor Train Matrix Format; Mach, Thomas; in A. Cangiani, R.L. Davidchack, E.H. Georgoulis, A. Gorban, J. Levesley, M.V. Tretyakov: Numerical Mathematics and Advanced Applications 2011 - Proceedings of ENUMATH 2011, the 9th European Conference on Numerical Mathematics, Leicester : Springer; 2012. accepted, available as preprint MPIMD/11-09, 11 pages. |
@InProceedings{MacS12, author = {T. Mach and J. Saak}, title = {How Competitive is the ADI for Tensor Structured Equations?}, journal = {PAMM}, volume = {12}, number = {1}, publisher = {WILEY-VCH Verlag}, issn = {1617-7061}, year = {2011}, note = {DOI: 10.1002/pamm.201210306}, } | How Competitive is the ADI for Tensor Structured Equations?; Mach, Thomas; Saak, Jens; Proceedings in Applied Mathematics and Mechanics : Wiley InterScience; 2012. Pages: 635–636, DOI: 10.1002/pamm.201210306. |
@article {BenM11d, author = {P. Benner and T. Mach}, title = {Locally Optimal Block Preconditioned Conjugate Gradient Method for Hierarchical Matrices}, journal = {PAMM}, volume = {11}, number = {1}, publisher = {WILEY-VCH Verlag}, issn = {1617-7061}, url = {https://dx.doi.org/10.1002/pamm.201110360}, doi = {10.1002/pamm.201110360}, pages = {741--742}, year = {2011}, } | Locally Optimal Block Preconditioned Conjugate Gradient Method for Hierarchical Matrices; Benner, Peter; Mach, Thomas; Proceedings in Applied Mathematics and Mechanics : Volume 11, Issue 1, pages 741–742, December 2011; Wiley InterScience; 2011. DOI: 10.1002/pamm.201110360. |
@TECHREPORT{MPIMD11-12, author = {Thomas Mach, Jens Saak}, title = {Towards an ADI iteration for Tensor Structured Equations}, institution = {Max Planck Institute Magdeburg Preprints}, year = 2011, number = {MPIMD/11-12}, month = {December} } | Towards an ADI iteration for Tensor Structured Equations; Mach, Thomas; Saak, Jens; Max Planck Institute Magdeburg Preprints, MPIMD/11-12; 2011. 16 pages. |
@ARTICLE{BenM10, author = {Peter Benner and Thomas Mach}, title = {{O}n the {QR} {D}ecomposition of $\mathcal{H}$-{M}atrices}, year = {2010}, journal = {Computing}, volume = {88}, number = {3--4}, pages = {111--129} } | On the QR Decomposition of ℋ-Matrices; Benner, Peter; Mach, Thomas; Computing : Vol. 88, No. 3-4, pp. 111-129; Springer; 2010. DOI: 10.1007/s00607-010-0087-y see also CSC preprint 09-04. |
| 154 | Computing the Eigenvalues of Hierarchical Matrices by LR-Cholesky Transformations; Benner, Peter; Mach, Thomas; Mathematisches Forschungsinstitut Oberwolfach, Report No. 37/2009, pp. 325-328; Mathematisches Forschungsinstitut Oberwolfach; 2009. DOI: 10.4171/OWR/2009/37. |